Sora Generates Videos with Stunning Geometrical Consistency

Xuanyi LI*1 , Daquan ZHOU *2, Chenxu ZHANG 2 Shaodon WEI 3 Qibin HOU 1 Ming-Ming CHENG 1
1VCIP, Nankai University 3Wuhan University 
2ByteDance Inc  
arXiv Code

Comparisons among Sora, Pika, and Gen2. (a) shows the quantitative evaluations across five metrics, which we define in Sec. 2. For more details, readers can refer to Tab. 1. (b) presents the performance of different methods under our designed Sustained Stability metric. For both figures, we can see a significant advantage of Sora over other baselines in terms of geometry consistency.

Abstract

The recently developed Sora model [1] has exhibited remarkable capabilities in video generation, sparking intense discussions regarding its ability to simulate real-world phenomena. Despite its growing popularity, there is a lack of established metrics to evaluate its fidelity to real-world physics quantitatively. In this paper, we introduce a new benchmark that assesses the quality of the generated videos based on their adherence to real-world physics principles. We employ a method that transforms the generated videos into 3D models, leveraging the premise that the accuracy of 3D reconstruction is heavily contingent on the video quality. From the perspective of 3D reconstruction, we use the fidelity of the geometric constraints satisfied by the constructed 3D models as a proxy to gauge the extent to which the generated videos conform to real-world physics rules.

Method

3D reconstruction pipeline

We refrain from modifying the original COLMAP [14] and Gaussian Splatting [18] algorithms to accommodate the characteristics of the generated videos. We utilize Structure-from-Motion (SfM) [14] to compute camera poses and then employ Gaussian Splatting for 3D reconstruction. The detailed metrics used in this benchmark are described in the following.

Metrics design

The foundational principle of SFM (Structure from Motion) [14] and 3D construction is multi-view geometry, meaning that the quality of the model relies on two main factors: 1) The perspectives of the virtual video’s observation cameras must sufficiently meet physical characteristics, such as the pinhole camera; 2) As the video progresses and perspectives change, the rigid parts of the scene must vary in a manner that maintains physical and geometric stability. Furthermore, the fundamental unit of multi-view geometry is two-view geometry. The higher the physical fidelity of the AI-generated video, the more its two frames should conform to the ideal two–view geometry constraints, such as epipolar geometry. Specifically, the more ideal the camera imaging of the virtual viewpoints in the sequence video, the more faithfully the physical characteristics of the scene are preserved in the images. The closer the two frames adhere to ideal two–view geometry, and the smaller the distortion and warping of local features in terms of grayscale and shape, the more matching points can be obtained by the matching algorithm. Consequently, a higher number of high-quality matching points are retained after RANSAC [19]. Therefore, we extract two frames at regular intervals from the AI-generated videos, yielding pairs of two-view images. For each pair, we use a matching algorithm to find corresponding points and employ RANSAC based on the fundamental matrix (epipolar constraint) to eliminate incorrect correspondences. 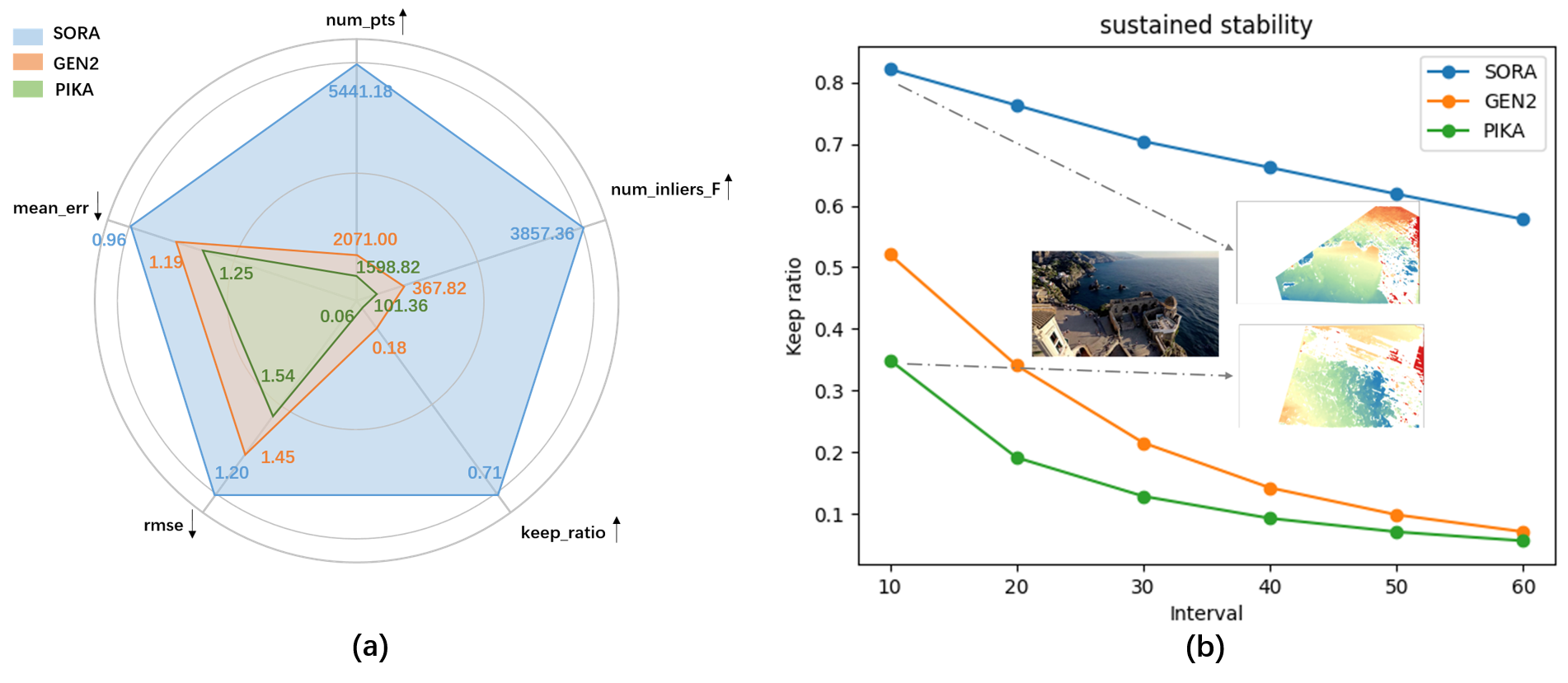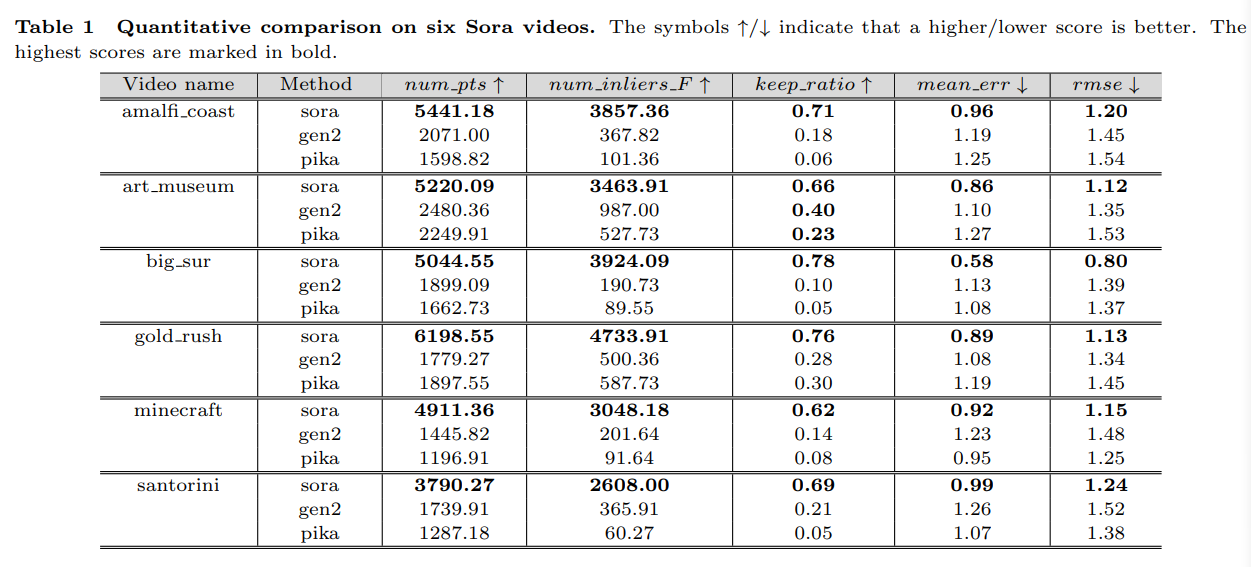After elimination, we calculate the average number of correct initial matching points, the average number of retained points, and the average retention ratio. 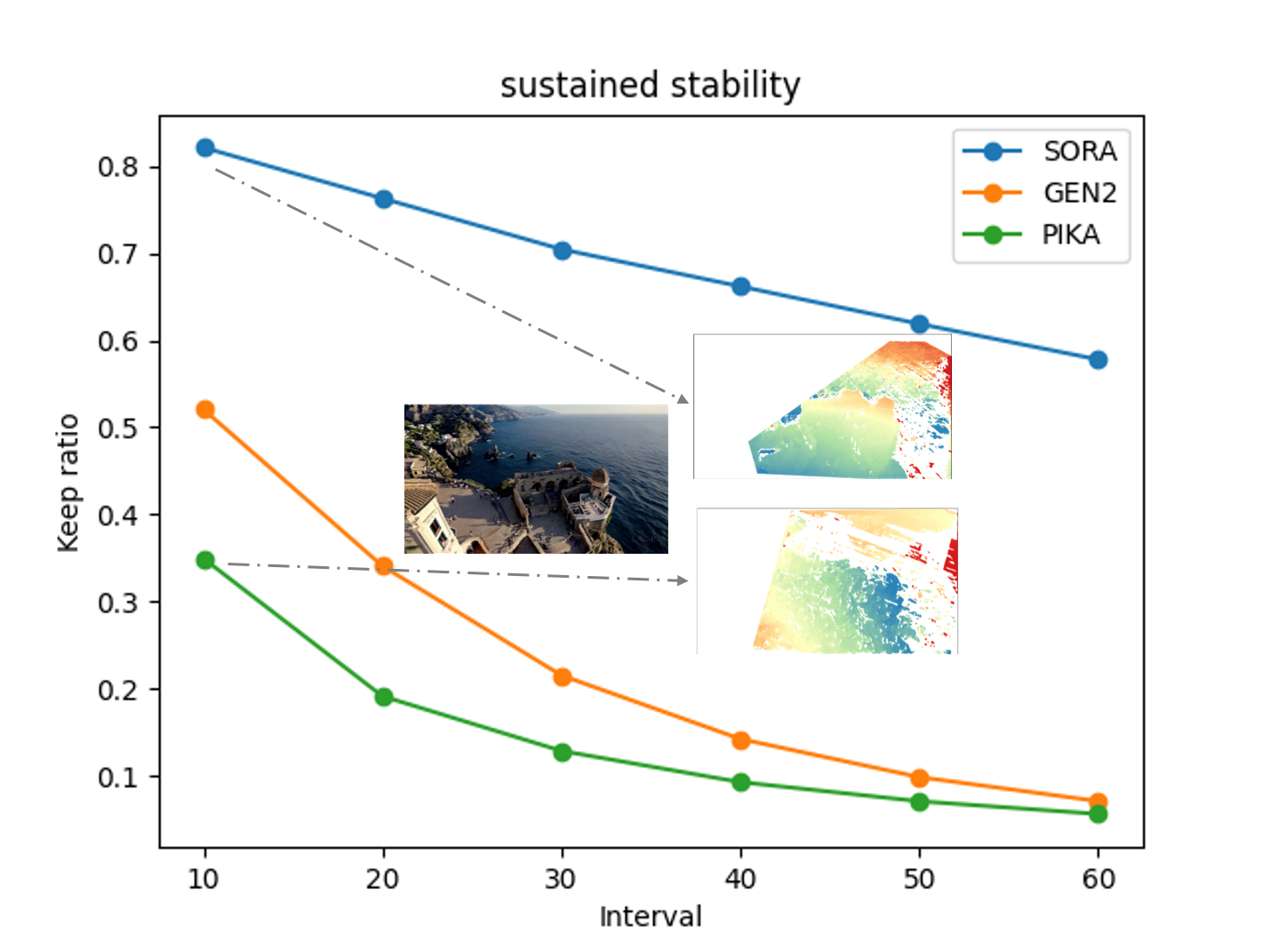Therefore, we have the following metrics: num pts refers to the total number of initial matching points in the binocular view, and num inliers F refers to the total number of matching points retained after filtering. The keep ratio is obtained by the ratio of num inliers F to num pts. Additionally, for each pair of images, we calculate the bidirectional geometric reprojection error for N matching points per point of the F matrix, d(x, x′). x and x′ are the matching points retained after RANSAC and d is the distance from a point to its corresponding epipolar line. Finally, we perform an overall statistical analysis of all data to calculate the RMSE (Root Mean Square Error) and MAE (Mean Absolute Error).

Results

1. Fidelity metric result

2. Sustained stability metric result

3. Visualization and Comparison of 3D Reconstruction Results from Different Videos Generation Methods

4. Visualization and Comparison of sparse matching Results from Different Videos Generation Methods

5. Visualization and Comparison of stereo matching Results from Different Videos Generation Methods

6. Visualization Comparison of Videos Generated by Different Methods (pika --> gen2 --> sora)

BibTeX

If this paper is useful or relevant to your research, please kindly recognize our contributions by citing our paper: 

@article{XuanyiLI2024Sora,
  title={ Sora Generates Videos with Stunning Geometrical
    Consistency},
  author={Xuanyi LI, Daquan ZHOU, Chenxu ZHANG, Shaodong Wei,  Qibin HOU, Ming-Ming CHENG},
  journal={arXiv preprint arXiv: 2402.17403},
  year={2024}
}